background

DQN solves problems with high-dimensional observation spaces, it can only handle discrete and low-dimensional action spaces. Many tasks of interest, most notably physical control tasks, have continuous (real valued) and high dimensional action spaces. DQN cannot be straight- forwardly applied to continuous domains since it relies on a finding the action that maximizes the action-value function, which in the continuous valued case requires an iterative optimization process at every step.

将DQN应用到连续动作空间的改进方法：将连续空间离散化，1.带来指数形式的维度灾难的问题；2.无法高效的进行探索开发，3.丢失连续空间本身的结构信息，不利于求解问题。

本论文解决方案：基于deterministic policy gradient (DPG)

Deep DPG (DDPG)

model-free, off-policy ,actor-critic algorithm, using deep function approx- imators that can learn policies in high-dimensional, continuous action spaces.

Prior to DQN, it was generally believed that learning value functions using large, non-linear function approximators was difficult and unstable. DQN is able to learn value functions using such function approximators in a stable and robust way due to two innovations:

• the network is trained off-policy with samples from a replay buffer to minimize correlations between samples;
• the network is trained with a target Q network to give consistent targets during temporal difference backups.
• In this work we make use of the same ideas, along with batch normalization (Ioffe & Szegedy, 2015), a recent advance in deep learning.

A key feature of the approach is its simplicity: it requires only a straightforward actor-critic archi- tecture and learning algorithm with very few “moving parts”, making it easy to implement and scale to more difficult problems and larger networks.

Detail:

The DPG algorithm maintains a parameterized actor functionμ(s|θμ)which specifies the current policy by deterministically mapping states to a specific action. The criticQ(s, a)is learned using the Bellman equation as in Q-learning. The actor is updated by following the applying the chain rule to the expected return from the start distributionJwith respect to the actor parameters:

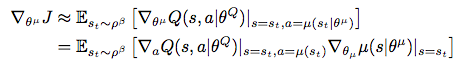
As with Q learning, introducing non-linear function approximators means that convergence is no longer guaranteed. However, such approximators appear essential in order to learn and generalize on large state spaces.

One challenge when using neural networks for reinforcement learning is that most optimization al- gorithms assume that the samples are independently and identically distributed. Obviously, when the samples are generated from exploring sequentially in an environment this assumption no longer holds. Additionally, to make efficient use of hardware optimizations, it is essential to learn in mini- batches, rather than online.

• DDPG is an off-policy algorithm, the replay buffer can be large, allowing the algorithm to benefit from learning across a set of uncorrelated transitions.
• Our solution is similar to the target network used in (Mnih et al., 2013) but modified for actor-critic and using “soft” target updates, rather than directly copying the weights.The weights of these target networks are then updated by having them slowly track the learned networks:θ′←τθ+ (1−τ)θ′withτ≪1. This means that the target values are constrained to change slowly, greatly improving the stability of learning. This simple change moves the relatively unstable problem of learning the action-value function closer to the case of supervised learning, a problem for which robust solutions exist.the target network delays the propagation of value estimations. However, in practice we found this was greatly outweighed by the stability of learning.
• manually scale the features so they are in similar ranges across environments and units. We address this issue by adapting a recent technique from deep learning calledbatch normalization
• In the low-dimensional case, we used batch normalization on the state input and all layers of theμnetwork and all layers of theQnetwork prior to the action input
• exploration. An advantage of off- policies algorithms such as DDPG is that we can treat the problem of exploration independently from the learning algorithm. We constructed an exploration policyμ′by adding noise sampled from a noise processNto our actor policy 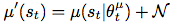.Ncan be chosen to chosen to suit the environment. As detailed in the supplementary materials we used an Ornstein-Uhlenbeck process (Uhlenbeck & Ornstein, 1930) to generate temporally corre- lated exploration for exploration efficiency in physical control problems with inertia (similar use of autocorrelated noise was introduced in (Wawrzyn ́ski, 2015)).