DDPG,DQN等常规方法记忆回放的缺点

  • Deep RL algorithms based on experience replay have achieved unprecedented success in challenging domains such as Atari 2600. However, experience replay has several drawbacks: it uses more memory and computation per real interaction; and it requires off-policy learning algorithms that can update from data generated by an older policy.

改进：

Instead of experience replay, we asynchronously execute multiple agents in parallel, on mul- tiple instances of the environment. This parallelism also decorrelates the agents’ data into a more stationary process, since at any given time-step the parallel agents will be ex- periencing a variety of different states. This simple idea enables a much larger spectrum of fundamental on-policy RL algorithms, such as Sarsa, n-step methods, and actor- critic methods, as well as off-policy RL algorithms such as Q-learning, to be applied robustly and effectively using deep neural networks.

相关工作：

  • 分布式actor-critic：Each process contains an actor that acts in its own copy of the environment, a separate replay memory, and a learner that samples data from the replay memory and computes gradients of the DQN loss (Mnih et al.,2015) with respect to the policy parameters. The gradients are asynchronously sent to a central parameter server which updates a central copy of the model. The updated policy parameters are sent to the actor-learners at fixed intervals.

  • evolutionary meth- ods, which are often straightforward to parallelize by dis- tributing fitness evaluations over multiple machines or threads

value function：one-step Q-learning：

  • it's only one-step Q-learning because it updates the action value Q(s, a) toward the one- step return r+γmaxa′Q(s′, a′;θ). One drawback of us-ing one-step methods is that obtaining a reward r only directly affects the value of the state action pair s, a that led to the reward. The values of other state action pairs are affected only indirectly through the updated valueQ(s, a). This can make the learning process slow since many up- dates are required the propagate a reward to the relevant preceding states and actions.
  • One way of propagating rewards faster is by usingn- step returns。 In n-step Q-learning,Q(s,a)is updated toward then- step return defined asrt+γrt+1+· · ·+γn−1rt+n−1+ maxaγnQ(st+n,a). This results in a single rewardrdi- rectly affecting the values ofnpreceding state action pairs. This makes the process of propagating rewards to relevant state-action pairs potentially much more efficient.

policy method：

  • policy-based model- free methods directly parameterize the policyπ(a|s;θ)and update the parametersθby performing, typically approx- imate, gradient ascent on E[Rt].
  • Standard REINFORCE updates the policy parameters θ in the direction ∇θlogπ(at|st;θ)Rt,which is an unbiased estimate of ∇θE[Rt]. It is possible to reduce the variance of this estimate while keeping it unbi- ased by subtracting a learned function of the statebt(st), known as a baseline (Williams,1992), from the return. The resulting gradient is ∇θlogπ(at|st;θ) (Rt−bt(st)).

  • A learned estimate of the value function is commonly used as the baseline bt(st)≈Vπ(st) leading to a much lower variance estimate of the policy gradient.

  • When an approx- imate value function is used as the baseline, the quantity Rt−bt used to scale the policy gradient can be seen as an estimate of the advantage of action at in statest, or A(at, st) =Q(at, st)−V(st), because Rt is an estimate of Qπ(at,st) and bt is an estimate of Vπ(st). Thisapproach can be viewed as an actor-critic architecture where the pol- icy π is the actor and the baseline bt is the critic

Detail：

  • 1.asynchronous actor-learners，use multi- ple CPU threads on a single machine. Keeping the learn- ers on a single machine removes the communication costs of sending gradients and parameters.
  • 2.actor-learners running in parallel are likely to be exploring dif- ferent parts of the environment. Moreover, one can explic- itly use different exploration policies in each actor-learner to maximize this diversity. By running different explo- ration policies in different threads, the overall changes be- ing made to the parameters by multiple actor-learners ap- plying online updates in parallel are likely to be less corre- lated in time than a single agent applying online updates. Hence, we do not use a replay memory and rely on parallel actors employing different exploration policies to perform the stabilizing role undertaken by experience replay in the DQN training algorithm.
  • 3.First, we ob- tain a reduction in training time that is roughly linear in the number of parallel actor-learners. Second, since we no longer rely on experience replay for stabilizing learning we are able to use on-policy reinforcement learning methods such as Sarsa and actor-critic to train neural networks in a stable way.

Asynchronous Methods

  • asynchronous advantage actor-critic (A3C),maintains a policyπ(at|st;θ)and an estimate of the value functionV(st;θv).

  • Each n-step update uses the longest possible n-step return resulting in a one-step update for the last state, a two-step update for the second last state, and so on for a total of up totmaxupdates. The accumulated updates are applied in a single gradient step.

  • The policy and the value function are updated after everytmaxactions or when a terminal state is reached. The update performed by the algorithm can be seen as ∇θ′logπ(at|st;θ′)A(st, at;θ, θv) whereA(st, at;θ, θv)is an estimate of the advantage func-tiongivenby 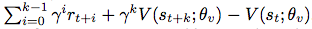wherekcan vary from state to state and is upper-bounded by tmax.

  • while the parametersθof the policy andθvof the value function are shown as being separate for generality, we always share some of the parameters in practice. We typically use a convolutional neural network that has one softmax output for the policyπ(at|st;θ)and one linear output for the value functionV(st;θv), with all non-output layers shared.

  • We also found that adding the entropy of the policyπto the objective function improved exploration by discouraging premature convergence to suboptimal deterministic poli- cies.

  • The gradi- ent of the full objective function including the entropy regularization term with respect to the policy parame- ters takes the form∇θ′logπ(at|st;θ′)(Rt−V(st;θv)) +β∇θ′H(π(st;θ′)), whereHis the entropy. The hyperpa- rameterβcontrols the strength of the entropy regulariza- tion term.

  • Optimization:We investigated three different optimiza- tion algorithms in our asynchronous framework – SGD with momentum, RMSProp (Tieleman & Hinton,2012) without shared statistics, and RMSProp with shared statis- tics.

  • A com- parison on a subset of Atari 2600 games showed that a vari- ant of RMSProp where statistics g are shared across threads is considerably more robust than the other two methods.

results matching ""

    No results matching ""