Background

技术发展的推动因素：

1、compute 计算力（cpu，gpu）

2、data 数据集（带标签的大型数据集）

3、新的算法（CNN, LSTM）

4、infrastructure 基础架构（software under you - Linux, TCP/IP, Git, ROS, PR2, AWS, AMT, TensorFlow）

很大程度来说，当前取得极大进步的强化学习算法依旧是几十年前已有的标准组件（q-learning，policy gradient），主要原因是compute/data/infrastructure.

策略梯度policy gradient：PG is preferred because it is end-to-end: there’s an explicit policy and a principled approach that directly optimizes the expected reward.

端到端的将状态映射到动作，可输出离散动作的不同概率，或者连续动作。

游戏环境pong：we receive an image frame (a210x160x3byte array (integers from 0 to 255 giving pixel values)) and we get to decide if we want to move the paddle UP or DOWN (i.e. a binary choice). After every single choice the game simulator executes the action and gives us a reward: Either a +1 reward if the ball went past the opponent, a -1 reward if we missed the ball, or 0 otherwise. And of course, our goal is to move the paddle so that we get lots of reward.

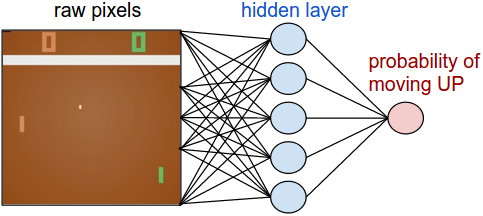
Policy network. First, we’re going to define a policy network that implements our player (or “agent”). This network will take the state of the game and decide what we should do (move UP or DOWN). As our favorite simple block of compute we’ll use a 2-layer neural network that takes the raw image pixels (100,800 numbers total (210*160*3)), and produces a single number indicating the probability of going UP. Note that it is standard to use a stochastic policy, meaning that we only produce a probability of moving UP. Every iteration we will sample from this distribution (i.e. toss a biased coin) to get the actual move. The reason for this will become more clear once we talk about training.

problem:1.credit assign :大量的参数，延迟稀疏的reward，上千step之后的reward如何更新权重

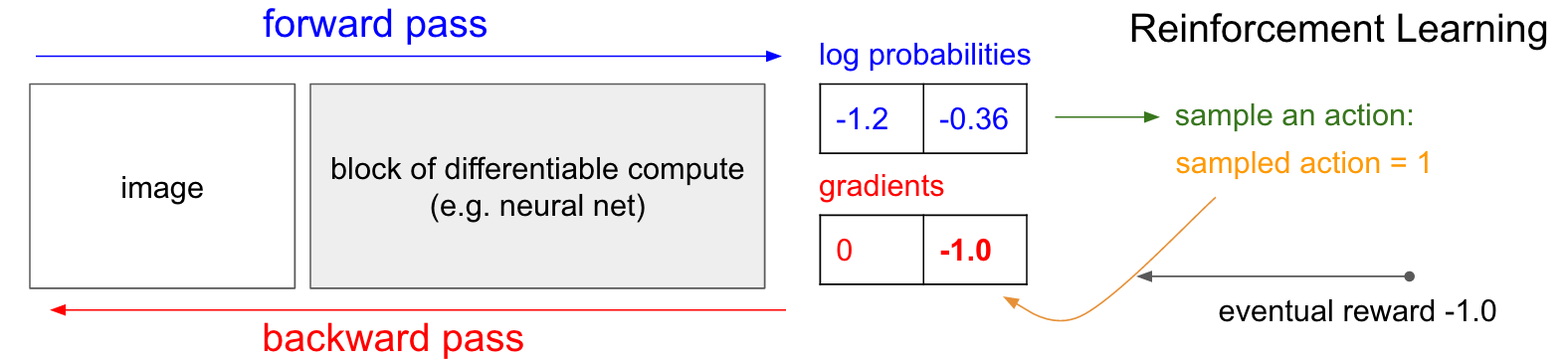And that’s it: we have a stochastic policy that samples actions and then actions that happen to eventually lead to good outcomes get encouraged in the future, and actions taken that lead to bad outcomes get discouraged. Also, the reward does not even need to be +1 or -1 if we win the game eventually. It can be an arbitrary measure of some kind of eventual quality. For example if things turn out really well it could be 10.0, which we would then enter as the gradient instead of -1 to start off backprop.

Non-differentiable computation in Neural Networks

It allows us to design and train neural networks with components that perform (or interact with) non-differentiable computation. The idea was first introduced in Williams 1992 and more recently popularized by Recurrent Models of Visual Attention under the name “hard attention”, in the context of a model that processed an image with a sequence of low-resolution foveal glances (inspired by our own human eyes). In particular, at every iteration an RNN would receive a small piece of the image and sample a location to look at next. For example the RNN might look at position (5,30), receive a small piece of the image, then decide to look at (24, 50), etc. The problem with this idea is that there a piece of network that produces a distribution of where to look next and then samples from it. Unfortunately, this operation is non-differentiable because, intuitively, we don’t know what would have happened if we sampled a different location. More generally, consider a neural network from some inputs to outputs:

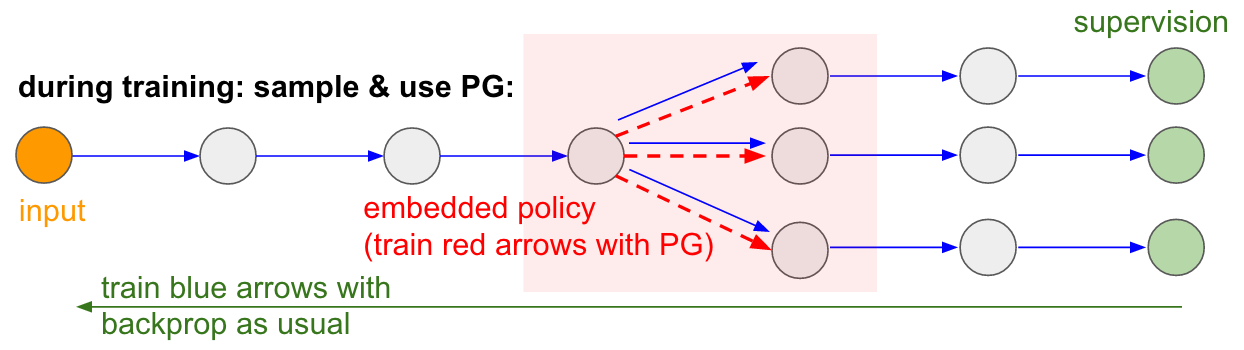
Policy gradients to the rescue! We’ll think about the part of the network that does the sampling as a small stochastic policy embedded in the wider network. Therefore, during training we will produce several samples (indicated by the branches below), and then we’ll encourage samples that eventually led to good outcomes (in this case for example measured by the loss at the end). In other words we will train the parameters involved in the blue arrows with backprop as usual, but the parameters involved with the red arrow will now be updated independently of the backward pass using policy gradients, encouraging samples that led to low loss. This idea was also recently formalized nicely in Gradient Estimation Using Stochastic Computation Graphs.

conclusion：However, with Policy Gradients and in cases where a lot of data/compute is available we can in principle dream big - for instance we can design neural networks that learn to interact with large, non-differentiable modules such as Latex compilers (e.g. if you’d like char-rnn to generate latex that compiles), or a SLAM system, or LQR solvers, or something. Or, for example, a superintelligence might want to learn to interact with the internet over TCP/IP (which is sadly non-differentiable) to access vital information needed to take over the world. That’s a great example.